MIKROTONAALSUST KAARDISTAMAS

Aprill, 2023

Võrdtempereeritud 22-helisüsteem

ANDRUS KALLASTU

Eesti Arnold Schönbergi Ühing on Pärnu nüüdismuusika päevadel kolm aastat süstemaatiliselt tegelnud mikrotonaalsusega. Kuigi eesti vanem rahvalaul on tihti mikrotonaalne ja eesti kunstmuusika esimesed kokkupuuted mikrotonaalsusega toimusid juba 1930. aastatel ning kuigi mikrotonaalsust on oma loomingus kasutanud nii mitmedki eesti heliloojad, ei ole selle teoreetilisi aspekte eesti keeles seni süstemaatiliselt ja ammendavalt käsitletud.

Mikrotonaalsust rakendavad muusikud näivad kuuluvat kolme suuremasse rühma: rahvustraditsioone esindavad „rahvamuusikud”, aeg-ajalt mikrointervallide abil võrdtempereeritud 12-helisüsteemi „maitsestavad muusikud” ja lõpuks „süstemaatikud”, kelle mikrointervallide kasutus põhineb teadlikel matemaatilistel valikutel. Elu ise on loomulikult mitmekesisem ja rikkam. Iga laulja või meloodiapilli mängija on kogenud, et võrdtempereeritud 12-helisüsteemis kirja pandud muusikat esitatakse kas puhtas häälestuses või puhast häälestust veidi kohandades, sest järjekindlalt võrdtempereeritud häälestust rakendades  ei kõla ansambel, koor või orkester lihtsalt muusiku kõrva jaoks piisavalt „puhtalt”.

Üksik heli ei saa olla mikrotonaalne. Mikrotonaalsusest on võimalik rääkida ainult helide seotud kogumis, helisüsteemis. ’Mikrotonaalsus’ (ingl k microtonality) on helisüsteemi  omadus põhineda võrdtempereeritud 12-helisüsteemis pooltoonist või selle kordsetest erinevatel intervallidel, mille kohta eesti keeles on kasutatud ka üldmõistet ’mikrointervall’. Kitsamas tähenduses on mikrointervallid võrdtempereeritud 12-helisüsteemis pooltoonist väiksemad „ultrakromaatilised” intervallid. Tänu modulo-operatsioonile, täpsemalt modulo 12vjo pooltoonile (vjo = võrdseks jagatud oktav), võib mikrointervallide hulka lugeda ka võrdtempereeritud 12-helisüsteemis pooltoonist suuremad „infrakromaatilised” intervallid. Intervallidega teostatav modulo-operatsioon põhineb modulaarsest aritmeetikast pärit täisarvude kongruentsuse kontseptsioonil. Täisarvud a ja b on kongruentsed ehk jäägivõrdsed, kui nad jagamisel mingi kindla naturaalarvuga n > 1 ehk mooduliga annavad võrdse jäägi, st kuuluvad samasse jäägiklassi n järgi: ab (mod n).

Kuna mikrotonaalsuse mõistega seotud terminoloogiline ebamäärasus uurijaid tihti ei rahulda, on näiteks Ameerika helilooja Ivor Darreg teinud ettepaneku kasutada mikrotonaalsuse tähenduses sõna ’ksenharmoonia’ (ingl k xenharmonic).

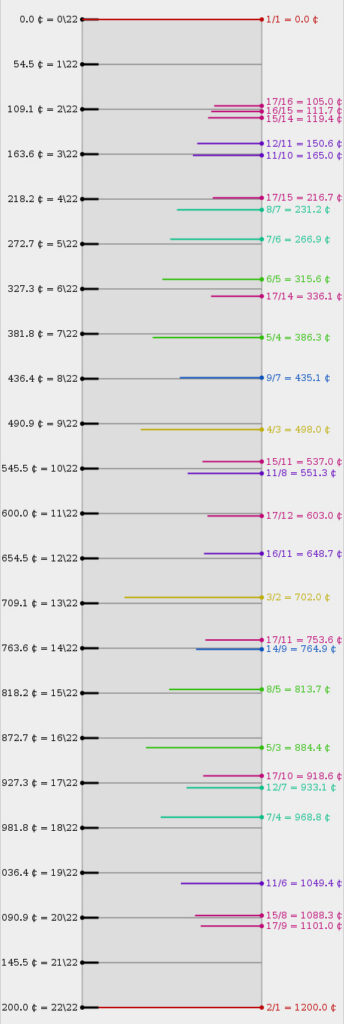
22vjo intervallide võrdlus puhtas häälestuses intervallidega. Vasakul on 22vjo skaala: astmete suurused logaritmilisel tsent-skaalal alates nullist. Võrdtempereeritud helisüsteemi astmete nimetusi tähistatakse: astme number (ingl k scale degree) — tagur­pidi kaldkriips (ingl k backslash) — nvjo väärtus n. Parempoolses veerus on 22vjo intervallile ligikaudsete paarituarvuliste limiit-17 puhaste intervallide väärtused esitatuna helisageduste naturaalarvuliste suhete ja logaritmilise tsent-skaala väärtustena.
(Allikas: Xenharmonic Wiki.)

 

Helisüsteem võib olla puhtas või ühes paljudest tempereeritud häälestustest. ’Puhas häälestus’ (ingl k just intonation) põhineb puhastel intervallidel, mida kirjeldavad helisüsteemi helide sageduste naturaalarvulised suhted. Puhtas häälestuses helisüsteemi etaloniks on harmoonilise liitheli osahelide süsteem, milles esimese lihtheli intervalli, priimi kirjeldab naturaalarvude suhe 1/1, teise lihtheli intervalli, oktavit 2/1,  kolmanda lihtheli intervalli, puhast kvinti 3/2 ning vastavalt edasi puhast kvarti 4/3, puhast suurt tertsi 5/4, puhast väikest tertsi 6/5, limiit-7 alumist väikest tertsi 7/6, limiit-7 tervetooni 8/7, puhast suurt tervetooni 9/8, puhast väikest tervetooni 10/9 jne. Sarnaselt naturaalarvude hulgaga on lõputu ka puhaste intervallide hulk. Kuna opereerimine lõpmatusega ei ole praktilises muusika tegemises arusaadavalt kuigi mõttekas, mõistetakse puhtas häälestuses helisüsteemi all tavaliselt ’puhtas häälestuses helide lõpliku arvuga alarühma’ (ingl k just intonation subgroup). Puhtal häälestusel põhineva, helide lõpliku arvuga alarühma näiteks on Pythagorase häälestus intervallidega vähendatud kvint 1024/729, väike sekund 256/243, väike sekst 128/81, väike terts 32/27, väike septim 16/9, puhas kvart 4/3, priim 1/1, puhas kvint 3/2, suur sekund 9/8, suur sekst 27/16, suur terts 81/64, suur septim 243/128 ja suurendatud kvart 729/512.

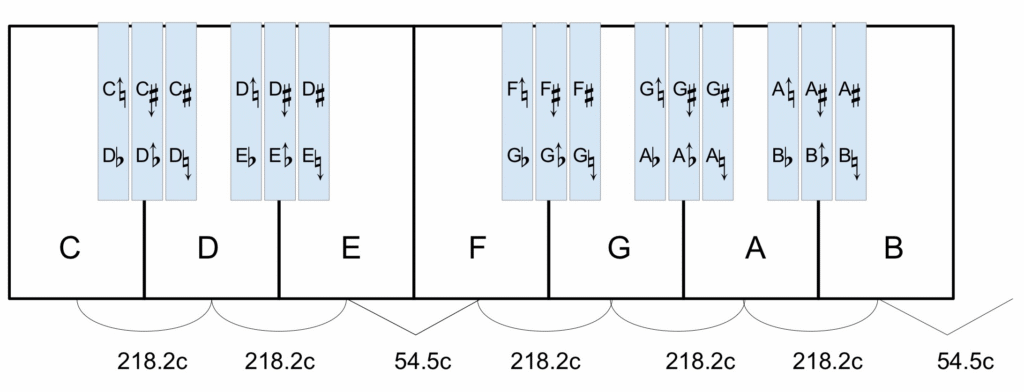
22vjo superpythagorase süsteemile C * * * D * * * E F * * * G * * * A * * * B C põhinev klaviatuurimudel. Tähed süsteemi kirjelduses tähistavad alushelisid, millele klaviatuuril vastavad n-ö valged klahvid. Tärnid süsteemi kirjelduses tähistavad alushelide alteratsioone, millele klaviatuuril vastavad n-ö mustad klahvid.

 

’Tempereeritud häälestus’ ehk ’temperatsioon’ (ingl k temperament) on puhta häälestuse modifikatsioon, mille loomiseks ja kasutamiseks on läbi ajaloo olnud erinevaid esteetilisi ja sotsiaalkultuurilisi põhjusi. Tempereeritud häälestused võivad olla regulaarsed või mitteregulaarsed. ’Regulaarne temperatsioon’ (ingl k regular temperament) põhineb kindlal, ühest või mitmest ’generaatorintervallist’ (ingl k generator) ja ’perioodintervallist’ (ingl k period) koosneval mudelil, mis peab andma võimaluse genereerida helisüsteemi kõiki helisid. Kui selline mudel puudub ning helisüsteemi iga intervalli tempereeritakse iseseisvalt, on tegu mitteregulaarse temperatsiooniga.

22vjo noodikiri, tähtnimetused ja intervallid. Joonisel on ära näidatud enharmooniliste helide C üles = Des, Cis alla = Des üles, Cis = D alla jne paarid. Samuti on välja toodud intervallide komplementaarsed paarid priim — oktav,
väike sekund — suur septim jne. Tervenoodiga on tähistatud alushelid.
Vasakpoolses veerus on esitatud 22vjo heliklassid.

 

Kasutaja mitteregulaarse temperatsiooni vajaduse on tavaliselt põhjustanud puhaste intervallide teatud kombinatsioonide konflikt, mis on muusikutel takistanud mõnede intervallide sujuvat uuel  moel rakendamist. Nii tõi näiteks renessanssheliloojate järjest kasvav huvi tertsi kui konsonantsi kasutamise vastu kaasa erinevate kesktoonhäälestuste tekke. Soov sujuvalt moduleerida ühest helistikust teise on aga põhjustanud näiteks võrdtempereeritud 12-helisüsteemi võidukäigu.

Puhtas häälestuses intervallide kombinatsioonide konflikti kehastuseks on spetsiifiline mikrointervall, ’komma’. Tehnilises mõttes võiks puhta häälestuse tempereerimist vaadelda komma teatud moel „jagamisena” helisüsteemi kõigi või osa intervallide vahel. Näiteks ’Pythagorase komma’ kehastab 12 puhta kvindi ja 7 oktavi konflikti. Liikudes kaksteist sammu puhaste kvintide ringi pidi üles, jõuame algheliga võrreldes helini intervalliga (3/2)¹², kuigi meie mõtteliseks sooviks oli jõuda helini intervalliga 2⁷. Nende kahe heli intervalli nimetataksegi Pythagorase kommaks suurusega (3/2)¹² / 2⁷ = 531441/524288 ehk umbes 23,46 tsenti.

 

Temperatsiooni poolt määratud helide intervallide omaduste võrdlemine toimub võrdluses puhtas häälestuses intervallidega. Nii kujutabki mikrotonaalsete helisüsteemide teooria lisaks eri temperatsioonide genereerimisele ka füüsikalis-matemaatiliste põhjenduste esitamist muusikute empiirilistele kogemustele näiteks intervallide konsoneerivusest või dissoneerivusest.

Temperatsioonide võrdlemiseks on erinevaid mõõdikuid, millest üks on temperatsiooni ’halbus’ (ingl k badness). Halbus on temperatsiooni ’vea’ (ingl k error) ja ’keerukuse’ (ingl k complexity) funktsioon: mida suurem halbus, seda vähem rahuldab temperatsioon puhta häälestuse etaloni.

Halbuse kvantitatiivseks mõõtmiseks on erinevaid lähenemisi, mis võivad anda erineva tulemuse. Kõik halbuse valemid võtavad siiski ühel või teisel moel muutujana arvesse temperatsiooni viga, st tempereeritud intervalli erinevust puhtas häälestuses etalonintervallist. Lähenemiste lahknevus on pigem arusaamises valemi teisest muutujast, keerukusest.

Ameerika helilooja, matemaatik ja muusikateoreetik Gene Ward Smith lähtub temperatsiooni struktuursest keerukusest: puhta häälestuse intervallist tempereerimisel tuletatud intervall on seda keerukam, mida suurem on puhtas häälestuses intervalli lähedusse jõudmiseks vajalike tempereeritud häälestuse generaatorintervalli sammude arv. Näiteks 12vjo septim on keerulisem kui kvint, kuna 12vjo septimi etaloniks oleva puhtas häälestuses septimi lähedusse jõudmine eeldab suuremat arvu 12vjo generaatorintervalliks oleva 12vjo pooltooni sammu kui 12vjo kvindi etaloniks oleva puhtas häälestuses kvindi lähedusse jõudmine.

Inglise arvutitarkavara insener Graham Breed lähtub keerukuse määramisel pigem tunnetuslikest aspekti­dest, sõnastades temperatsioonide võrdlemise põhimõtte järgmiselt: 1) naturaalarvulistel suhetel on soovitav mõju; 2) mida lähemal naturaalarvulistele suhtele, seda tugevam on soovitud mõju; 3) keskmised vead paistavad rohkem silma kui väikesed; 4) suured vead ei oma tähtsust.

22vjo laadisüsteemid ja helilaadid. Laadisüsteemi nimetuses sõnaline osa viitab temperatsioonile ja nurksulgudes olev number tähistab laadisüsteemi astmete arvu. Laadi struktuur on määratud järjestatud numbritega, mis tähistavad astmete laiusi. Kolm punkti tähistavad laadisüsteemi ülejäänud laade.

 

Mikrointervallidega tegelemine esitab tavapärase lääne hariduse saanud muusikule matemaatilise väljakutse.

Kui tavaline muusikakoolis õpetatav muusikateooria opereerib mõistega ’helikõrgus’ (ingl k pitch) kui millegi kindlalt fikseerituga, siis mikrotonaalsusega tegeldes jääb sellest väheks. Ilmneb, et helikõrgus on muusikaline parameeter, millele omistatud väärtus sõltub konventsioonist. Seda on täheldanud juba ka veidi laiema silmaringiga muusikud, kelle jaoks kammertoon, 1. oktavi la võib olla standardses MIDI-häälestuses 440 hertsi, tänapäeva sümfooniaorkestri häälestuses 442 või isegi 443 hertsi või hoopis 435 hertsi, mille järgi mõnikord häälestatakse ajalooliselt informeeritud esitusteadlikke barokkorkestreid. Pärnu nüüdismuusika päevadel võrdtempereeritud 22-helisüsteemiga tegeldes tegime meie otsuse, et kammertoon on hoopis 1. oktavi do helisagedusega 261,626 hertsi, mis annab 1. oktavi la väärtuseks 446,987 hertsi.

Teine matemaatiline väljakutse on seotud mõistega ’intervall’. Koolimuusika teoorias räägitakse intervallist kui helikõrguste või heliastmete vahest, millel on vastavalt kas tooniline suurus, mida mõõdetakse tervetoonides, või astmeline suurus, mida tähistavad intervallide nimetused priim, sekund, terts jne. Mikrotonaalsusega tegeldes jääb intervallide mõõtmisel selline täpsus ebapiisavaks. Mikrointervalle kirjeldatakse ’helisageduste’ (ingl k frequency) suhete abil: puhtaid intervalle on võimalik kirjeldada naturaalarvuliste ning kõiki teisi intervalle muude reaalarvuliste suhete abil. Helisagedusi võrreldes on vaja tähele panna ka seda, et kui helikõrguse muutumisest räägitakse lineaarselt, siis helisagedus muutub tegelikult eksponentsiaalselt. Näiteks helikõrguse muutumine ühe oktavi võrra tähendab helisageduse muutumist kaks korda.

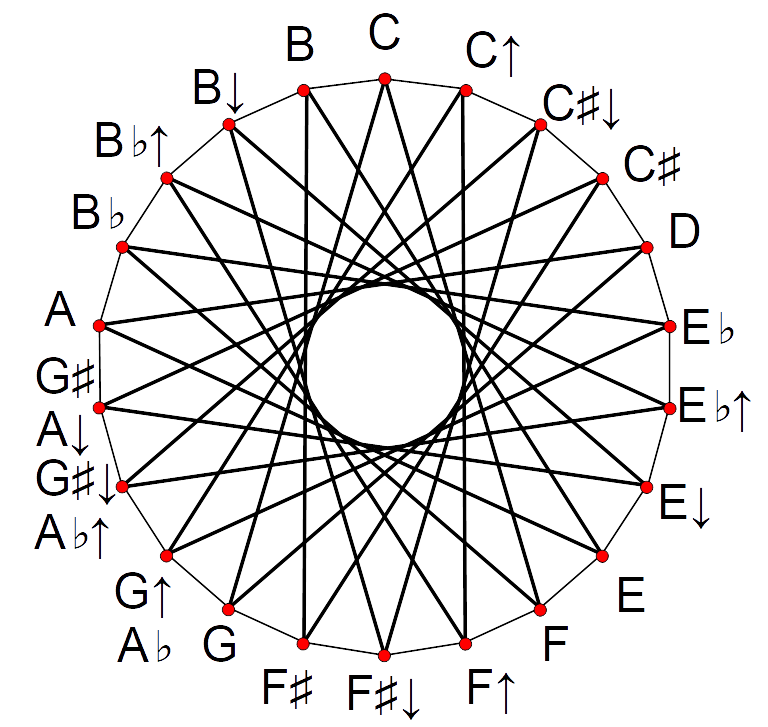
22vjo kvindiringist modulo oktav tuletatud 22vjo kromaatiline ring. 22vjo võimaldab harmoonilist moduleerimist 22 helistikku, atonaalsust ja 22-heliridade serialismi ehk ’ikosidifooniat’.

 

Kuna helisageduste intervallide võrdlemine eksponentsiaalsel skaalal võib olla muusikule matemaatiliselt keeruline, on kasutusele võetud mitmeid logaritmilisi skaalasid intervalli suuruse ülevaatlikumaks esitamiseks. Tuntuim neist on inglise matemaatiku, filoloogi ja foneetiku Alexander John Ellise 1875. aastal kasutusele võetud tsent-skaala, mille puhul oktav on jagatud logaritmiliselt 1200 võrdseks intervalliks suurusega 1 ’tsent’ (ingl k cent) ning mille puhul helisageduste suhte f₂/f₁ ümberarvutamine tsent-skaala intervalliks c toimub valemi järgi c = 1200 • log₂(f₂/f₁). Tsent-skaala tänaseni kestva populaarsuse põhjuseks võib arvatavasti pidada võrdtempereeritud 12-helisüsteemi domineerimist, mis on muutnud pooltooni suurusega 100 tsenti lääne muusiku jaoks mugavalt kasutatavaks intervallide võrdlemise etaloniks.

 

’Võrdtempereeritud häälestus’ (ingl k equal temperament) on regulaarse temperatsiooni erijuhtum, mille puhul mis tahes suurusega perioodintervall jagatakse võrdse suurusega intervallideks. Teisisõnu, võrdtempereeritud häälestuse genereerimiseks on vaja ainult ühte generaatorintervalli. See omadus liigitab võrdtempereeritud häälestused esimest ’järku’ (ingl k rank) regulaarsete temperatsioonide hulka. Võrdtempereeritud häälestust määravate generaatorintervalli ja häälestussüsteemi perioodintervalli suhet kirjeldab valem g = p^1/n, milles g on generaatorintervall, p on perioodintervall ning n on helisüsteemi helide arv.

’Võrdtempereeritud oktav’ (ingl k equal division of the octave, edo) ehk ’vjo’, „võrdselt jagatud oktav” on võrdtempereeritud häälestuste alaliik, milles perioodintervalliks on oktav. Üks kesksemaid mikrotonaalse muusikateooria tekstide korpusi Xenharmonic Wiki sisaldab artiklit võrdtempereeritud 6000000-helisüsteemist. Tõepoolest, perioodintervalli võrdseteks intervallideks jagamisel matemaatiline piir puudub, ainsa piiri seab inimese tajumisvõime.

 

* * *

’Võrdtempereeritud 22-helisüsteem’ (ingl k 22 equal divisions of the octave, lühendatult 22edo) ehk ’22vjo’ on võrdtempereeritud häälestuses helisüsteem, mis põhineb oktavi jagamisel kahekümne kaheks võrdseks intervalliks helisageduste suhtega kahekümne kahes juur kahest ehk 2^1/22 ehk umbes 54,55 tsenti.

Idee jagada oktav kahekümne kaheks võrdseks intervalliks tekkis 19. sajandi inglise  muusikateoreetikul Robert Holford Macdowall Bosanquet’l, kes sai selleks inspiratsiooni oktavi jagamisest kahekümne kaheks śruti’ks india muusikas. Siiski, võrdlus śruti’ga saab olla ainult viiteline, sest śruti’d kui „väikseimad intervallid, mida inimese kõrv suudab tuvastada ning mida laulja või muusikainstrument suudab tekitada” on üldjuhul erineva suurusega, põhinevad puhtal häälestusel ning iga konkreetse śruti suurus sõltub raagast, mille śruti’ga on tegu.

 

Võrdluses puhta häälestusega on 22vjo pärast 12- ja 19-vjo-d limiit-5 intervallide osas järgmine helisüsteem, milles temperatsiooni viga ühegi intervalli puhul ei ületa nelja tsenti. Enamgi veel, erinevalt 12- ja 19vjo-st jääb 22vjo temperatsiooni viga enamuse limiit-7 või limiit-11 intervallide puhul alla kolme tsendi. See on tempereerimisel juba väga võimas tulemus, sest ainult väga kogenud mikrotonaalsusega tegelejad on väitnud, et tajuvad helikõrguse 3-tsendist erinevust. Kuigi näiteks 31vjo on tempereerimisel veelgi täpsem, võimaldab juba ka 22vjo kasutada paljusid kõrgema limiidiga harmooniaid, sest tegu on väikseima võrdtempereeritud jaotusega, milles on järjekindlalt esindatud näiteks limiit-11 intervallid. Erinevalt võrdtempereeritud 12- ning 19vjo-st ei kuulu 22vjo kesktoonhäälestuste perekonda. Ühest küljest võimaldab see uurida vähem tuttavaid muusikalisi „territooriume”, mis teisest küljest on siiski piisavalt väiksed, et kasutada olemasolevaid või vaid vähesel määral ümber ehitatud akustilisi muusikainstrumente, nagu näiteks 22vjo-kitarr.

 

Siinkohal on ilmselt vaja selgitada mõistet ’limiit’ (ingl k limit), mis on Ameerika helilooja ja muusikateoreetiku Harry Partchi kasutusele võetud mõõdik helisüsteemi keerukuse kirjeldamiseks. Täpsuse huvides: Partch pidas oma teoorias vaikimisi silmas puhtas häälestuses intervalli ’paarituarvulist limiiti’ (ingl k odd limit), mille puhul leitakse intervalli esindava naturaalarvude suhte suurim paarituarvuline tegur. Tänapäeval räägitakse ka ’algarvulisest limiidist’ (ingl k prime limit, p-limit, p-prime-limit), mille puhul intervalli limiidiks on suurim algarvuline tegur.

Tempereeritud, sealhulgas võrdtempereeritud häälestuste puhul on intervalli limiidi määramiseks vaja tempereeritud intervalli vaadelda kõigepealt puhta intervalli kui etaloni ’lähendusena’ (ingl k approximation) ning seejärel tuvastada puhta intervalli limiit. Limiidi antud väärtust on seejärel võimalik kasutada tempereeritud intervalli iseloomustamiseks. Näiteks 22vjo väikest tertsi suurusega 272,727 tsenti nimetatakse ka 22vjo limiit-7 väikseks tertsiks selle lähendamise tõttu puhtale etalonintervallile, limiit-7 alumisele väiksele tertsile helisageduste suhtega 7/6 = 266,871 tsenti.

 

Mida suurem on helisüsteemi paarituarvuline limiit, seda rohkem on selles varem dissonantseid, kuid uue vaate järgi konsonantseks tunnistatud intervalle.

Keskaja Euroopa muusika põhines harmoonilise liitheli kolme esimese konsonantseks tunnistatud osaheli intervallidel: priimil 1/1, oktavil 2/1 ja kvindil 3/2. Järelikult oli keskaja muusika paarituarvuline limiit 3.

Renessansiajal tunnistati konsonantseks suur terts 5/4, mis tähendas konsonantseks tunnistatud osahelide piiri nihkumist viienda osahelini, hõlmates osahelisid intervallidega 1/1, 2/1, 3/2, 4/3 ja 5/4 . Kuna selle süsteemi suurimaks paarituarvuliseks teguriks on 5, oli renesanssmuusika paarituarvuline limiit 5.

 

20. sajandi alguses muutus afro­ameerika muusika mõjul järjest konsonantsemaks septakord. See tõi kaasa konsonantsena aktsepteeritud osahelide piiri järjekordse nihkumise. Näiteks 12vjo dominatseptakordi septim suurusega 1000 tsenti on lähendatav puhtas häälestuses harmoonilisele septimile helisageduste suhtega 7/4 = 968,826 tsenti. See tähendab, et dominantseptakordidel põhineva harmoonia paarituarvuline limiit kasvas 7-ni. Džässmuusika kontekstis „pehmenesid” konsonantseks ka suured septakordid, mille 12vjo suur septim suurusega 1100 tsenti on lähendatav osahelirea 15. osaheli intervallile, puhtale suurele septimile väärtusega 15/8 = 1,088,269 tsenti. Suurtel septakordide konsonantseks muutumine kasvatas harmoonia paarituarvulise limiidi juba 15-ni.

 

Kuna suur osa mikrotonaalsuse süstemaatilisest uurimisest jääb eelmisesse kolme aastakümnesse, ei ole veel arusaadavalt välja kujunenud ühte läbivat mikrotonaalsuse terminoloogiat ja noodikirja. Seetõttu on vaid teatud lahenduste esitlemine paratamatult subjektiivne. 

Kuigi on ka muid süsteeme, on 22vjo levinumaks noodinimede süsteemiks diatoonilistel alushelidel põhinev süsteem ’superpythagoras’ (ingl k superpyth) C * * * D * * * E  F * * * G * * * A * * * B C, milles tähed tähistavad alushelisid ja tärnid alteratsioone. Eestis on võimalik mugavama solfedžeerimise huvides tähtnimetustele lisaks kasutada ka do-re-mi-süsteemis silpnimetusi, asendades tähtnimetuse tavapärasel moel silpnimetusega C = do jne.

22 vjo helikõrguste ülesmärkimiseks noodikirjas on erinevaid võimalusi, kuid tavaliselt kasutatakse 5-joonelist noodijoonestikku ja standardseid noodimärke. Alteratsioonimärkide graafi-
line kuju sõltub eelkõige helilooja käsutuses olevast noodikirjaprogrammist või ka lihtsalt harjumusest teatud noodikirja märke eelistada. Näiteks minu kui programmi Finale kasutaja jaoks on mugav ’noolnoodikiri’ (ingl k ups and downs notation), milles tavapärasele alteratsioonimärgile lisatud üles- või allanooleke tugevdab või nõrgendab alteratsioonimärgi mõju.

Ka 22vjo intervallide nimetustel on mitu süsteemi. Mina olen pidanud loogiliseks noolnoodikirjast lähtuvat, selgeid intervallide komplementaarseid paare moodustavate nimetuste süsteemi, näiteks priim — oktav, väike sekund — suur septim, suurem väike sekund — väiksem suur septim jne. Selle süsteemi puuduseks võib olla kohatine tunnetuslik „noodipildi ja kõrva vastuolu” puhtas häälestuses intervallidega, mistõttu pean täiesti relevantseks kasutada ka näiteks nimetusi, mis põhinevad võrdlustel puhtas häälestuses intervallidega.

 

22vjo omab helilooja jaoks tunnetuslikult erinevat kõlalist koloriiti võrreldes harjumuspärase 12vjo-ga. Siiski võimaldab see struktuurses mõttes kasutada ära paljusid 12vjo ajaloolisi lähenemisi ja kompositsioonimeetodeid. 22vjo-s on olemas praktiliselt kõik 12vjo kompositsioonilised võimalused, kuid palju avaramalt, tundlikumalt ja täpsemalt.

 

Mikrotonaalsuse teoreetikute üheks põhjalikumalt uuritud ja heliloomingus rakendatud suunaks on 22vjo modaalsus. Kui 12vjo puhul me räägime põhiliselt penta-, heksa-, hepta-, okta- ja dodekatoonilistest laadisüsteemidest ning eristame seejuures põhiliselt diatoonikat ja kromaatikat, on 22vjo võimalused laadisüsteeme ehitada veelgi mitmekesisemad.  

22vjo superpythagoras on diatooniline laadisüsteem, mis põhineb ainult alushelidel C, D, E, F, G, A, B. Sarnaselt Pythagorase häälestusele ja näiteks 12vjo diatoonikale ehitub see ainult kvintidest. Kuna 22vjo kvindid on laiemad kui 12vjo või isegi puhtas häälestuses kvindid, on see süsteem saanud hinnangulise eesliite „super”. Tõepoolest, kuna 22vjo kvindid kõlavad isegi puhaste kvintidega võrreldes eriti kirkalt, peaks nende intoneerimine olema naudinguline isegi 22vjo suhtes skeptilisele lääne muusikule. 

Omaette laadisüsteemide kogumi moodustab ühisosa 11vjo laadisüsteemidega, mille hulka kuuluvad näiteks „masin[6]” (ingl k machine hexatonic), „orgone[7]” (ingl k orgone heptatonic), „joan[5]” (ingl k joan pentatonic), „joan[7]” (ingl k joan heptatonic) ja „joan[9]” (ingl k joan nonatonic). Mikrotonaalseid laadisüsteeme ja nendest tuletatud laade tähistatakse nimetustega, milles sõnaline osa viitab temperatsioonile, nurksulgudes number tähistab laadisüsteemi astmete arvu ning pärast nurksulge numbrid helilaadi astmete laiusi: näiteks „joan[5] 28282” (11vjo helisüsteemis vastab sellele joan[5] 14141) viitab joan-temperatsiooni kuuluvale 5-astmelises laadisüsteemis genereeritud helilaadile 22vjo astmete suurustega 2,8,2,8,2. Nagu 12vjo puhul, tuleb ka mikrotonaalsete laadide puhul teha vahet mõistetel ’laadisüsteem’ ja ’helilaad’. Laadisüsteem on astmete järjestamata hulk, helilaad on laadisüsteemist tuletatud järjestatud astmete rotatsioon.

Kolmas ja põhiline laadisüsteemide kogum on rohkemal või vähemal määral 22vjo-spetsiifiline. Sinna kuuluvad näiteks „orwelli” (orwell), „okassea” (ingl k porcupine), „siili” (ingl k hedgehog), „padžara” (ingl k pajara), „topeltlaia” (ingl k doublewide), „astroloogia” (ingl k astrology) ning „maagilise” (ingl k
magic) temperatsiooni laadisüsteemid.

 

Mikrotonaalususe teoreetikute jaoks on helilaadide uurimisel oluliseks küsimuseks olnud ka helilaadi momentsümmeetria tuvastamine. ’Momentsümmeetria’ (ingl k moment of symmetry, MOS) on Mehhiko/Ameerika muusikateoreetiku Erv Wilsoni 1975. aastal sõnastatud helilaadi omadus, mille kohaselt helilaadi astmelisi suurusi, üldistatult „suur, s” (ingl k large, L) ja „väike, v” (ingl k small, s), peab esindama täpselt kaks erinevat ühisteguriteta arvu. Teatud helisüsteemis laadisüsteemist momentsümmeetrilise helilaadi genereerimiseks peab astmete väärtusi genereerima generaatorintervall või -intervallid, mida helilaadi esimesest astmest alates järgmistele liites saadakse modulo laadisüsteemi perioodintervall, helilaadi astmete lõplik järjestus ja väärtused. Ka generaator­intervalli ja perioodintervalli peavad esindama ühisteguriteta arvud.

 

22vjo võimaldab hõlpsalt ka tonaalsete struktuuride loomist. Näiteks on 22vjo nelja tertsi hulgas väiksem terts ja väiksem suur terts, mida juba 12vjo-ga harjunud muusik võib tunnetuslikult pidada vastavalt minoorseks ja mažoorseks. See võimaldab ehitada kohati küll veidi kummaliselt kõlavaid, kuid siiski mažoorseid ja minoorseid heliridu, mistõttu me saame rääkida 22vjo duur-moll-süsteemist.

Samas pakub 22vjo kvint, mis on puhtas häälestuses kvindist veidi laiem, kuid tunnetuslikult siiski väga hästi konsoneeriv, lihtsa võimaluse rõhutada tonaalseid keskusi. See annab võimaluse mõelda 22vjo funktsionaalharmooniast: toonikast, subdominandist, dominandist.

22vjo, nagu iga teinegi võrdtempereeritud helisüsteem võimaldab ka meloodiate ja akordide kadudeta transponeerimist. Kombinatsioonis muude tonaalse harmoonia võimalustega võimaldab see omakorda nii funktsionaalseid kui ka elliptilisi kaldumisi ja modulatsioone eri helistikesse, mida 22vjo-s on loogiliselt 22.

Omamoodi kirev ja varjundirohke on ka 22vjo pakutav ’musica ficta’. Kui pidada muutumatuteks priimi ja kvinti, kuid anda interpreedile vabad käed valida sekundi, tertsi, kvardi, seksti ja septimi puhul nelja alteratsioonivariandi vahel, on võimalus mängida sama muusikalist materjali 1024-l erineval moel altereerides.

 

Nagu kõik võrdtempereeritud häälestused, sobib ka 22vjo suurepäraselt atonaalse muusika loomiseks nii selle vabades kui ka organiseeritud tehnikates. Samuti võimaldab see kõigi
12vjo-st tuttavate posttonaalse muusikaanalüüsi meetodite rakendamist. Näiteks seriaalse meetodi 22vjo rakendused sarnanevad 12vjo rakendustega. Erinevused on vaid mahtudes. „Ikosidifoonilisi” 22-heliridu on võimalik genereerida 22! = 1124000727777607680000. Võrdlusena: võimalike dodekafooniliste 12-heliridade arv on „vaid” 12! = 479001600.

22vjo, nagu kõik teised võrdtempereeritud häälestused, võimaldab enharmonismi: näiteks C üles = Des. Nii on ka 22vjo puhul rakendatav juba 12vjo-st tuttava heliklassihulkade teooria rikkalik tööriistakast. Sarnaselt 12vjo heliklassihulkade teooriale tähistatakse ka 22vjo heliklasse numbernotatsioonis 0 = C, 1= C üles / Des, 2 = Cis alla / Des üles kuni 20 = Ais / B alla, 21 = B.

 

Lõpetuseks võiks küsida, mida mikrotonaalsusega tegelemine standardse lääne hariduse saanud heliloojale või interpreedile annab. Üks vastuseid võiks olla: isegi mikrotonaalsust oma loomingus rakendamata on selle uuri­mine professionaalse muusiku jaoks pedagoogiliselt arendav. Piltlikult öeldes, see annab avarama mõtlemise, arusaamise, et ka „klaveri klahvide vahel” on helid.

 

Tänan häid kolleege nii Eestist kui ka välismaalt, kes on mind mikrotonaalsuse inspireeriva maailma juurde juhatanud ja teinud sellega võimalikuks ka käesoleva artikli. Eelkõige kuuluvad minu tänusõnad Hans-Gunter Lockile, keda võib täie õigusega pidada mikrotonaalsuse süstemaatilise uurimise ja rakendamise pioneeriks Eestis. Eesti Arnold Schönbergi Ühingu Pärnu nüüdismuusika päevade toimumine poleks olnud võimalik ilma Pärnu linna ja kultuurkapitali järjepideva rahalise toeta.

 

Allikad:

Eesti Arnold Schönbergi Ühingu koduleht. — https://schoenberg.ee/

Xenharmonic Wiki. — https://en.xen.wiki/w/Main_Page (Üks mahukamaid mikrotonaalsuse teemaliste ingliskeelsete materjalide kogumeid.)

Joseph Monzo. Tonalsoft. Encyclopedia of Microtonal Music Theory.

— http://tonalsoft.com/enc/ (Üks olulisemaid ühe autori loodud entsüklopeedilisi allikaid.)